Partons sur les bonnes bases
N’allez pas plus loin si vous ne maîtrisez pas ces connaissances basiques. Espérons qu’il ne s’agisse que d’un rappel… En tout cas, il est toujours bon de rappeler ces évidences, pour que sa mémoire reste structurée et organisée.
Algèbre
Fractions
Géométrie
Droites et segments
- Droite (AB)
- N’a pas de longueur et passe par A et B, illimité des deux côtés
- Segment [AB]
- Délimité par les extrémité A et B
- Demi-droite [AB)
- Possède une origine A et est illimité d’un seul côté en passant par B
Les triangles
Types de triangles
La somme des angles d’un triangle vaut 180° ()
- Triangle rectangle
- Possède un angle droit de 90° ().
- L’hypoténuse est le segment opposé à l’angle droit.
- Triangle isocèle
- Possède deux segments de même longueur.
- Triangle équilatéral
- Possède trois segments de même longueur et trois angles égaux à 60° ().
- Triangle scalène/quelconque
- Triangle qui ne possède aucun segments de même longueur, et sans angle droit.
Droites particulières d’un triangle
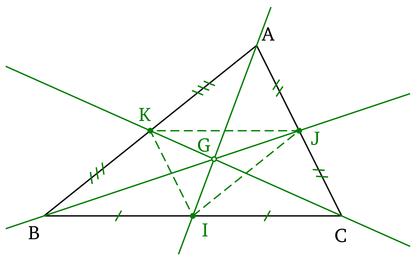
- Médiane
- Droite qui relie un sommet au milieu du côté opposé
- Les trois médianes se coupent au centre de gravité, sa distance avec les trois sommets est la même.
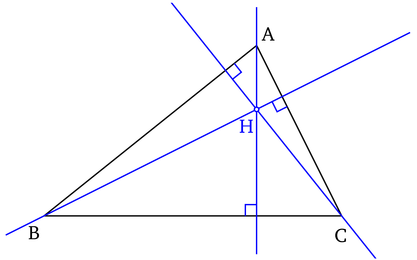
- Hauteur
- Droite qui relie un sommet au côté opposé en formant un angle droit
- Les trois hauteurs se coupent à l’orthocentre
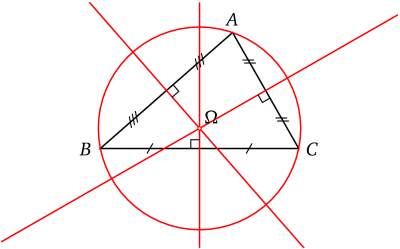
- Médiatrice
- Droite qui passe par le milieu d’un segment en formant un angle droit
- Les trois médiatrice se coupent au centre du cercle circonscrit, cercle passant par les trois sommets
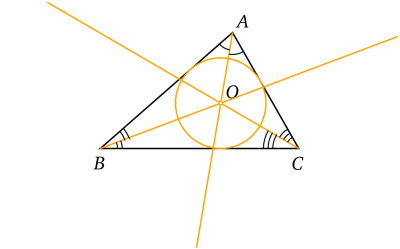
- Bissectrice
- Droite qui partage un angle de sommet en deux angles de même mesure
- Les trois bissectrices se coupent au centre du cercle inscrit
Triangle rectangle
Moyen mnémotechnique : SOH CAH TOA (prononcé “socatöa”)
Théorème de Pythagore
Le carré de l’hypoténuse est égal à la somme des carrés des deux autres côtés.
Théorème de Thalès
DE et BC sont parallèles alors :
Cercle trigonométrique

Propriétés d’un triangle rectangle avec une hypoténuse à 1 :

Les repères de plan
Un repère est :
- Orthogonal
- si et sont orthogonaux, formant un angle droit
- Orthonormé
- si et sont orthogonaux et de même norme,
- Direct
- si
- Indirect
- si
On distingue trois types de repères de plan qui correspondent à trois parties du programme :
- Repère orthonormé
- Utilisé pour les courbes et études de fonctions f(x)
- Un point M(x,y) possède les coordonnées x (abscisse sur ) et y (ordonnée sur )
- Repère orthonormé
- Utilisé pour la géométrie dans l’espace (trois dimensions)
- Un point M(x,y,z) a trois coordonnées dans l’espace
- Repère orthonormé dans le plan complexe
- Utilisé pour les représentations dans le plan complexe (en introduisant )
- Un point M(z) possède une affixe z
Analyse / Etude de fonctions
Courbes et fonctions
- Tangente
- La tangente à une courbe en un de ses points est une droite qui « touche » la courbe au plus près au voisinage de ce point. La courbe et sa tangente forment alors un angle nul en ce point.
- Asymptote
- L’asymptote est une tangente à l’infini. Lorsque l’abscisse ou l’ordonnée tend vers l’infini, la distance entre la courbe et l’asymptote tend vers 0.
Continuité
- Fonction continue
- Une fonction f est continue sur ssi admet une valeur.
- Fonction monotone
- Une fonction est monotone sur un intervalle, si elle est croissante/décroissante. On parle de strictement monotone/croissante/décroissante.
- Théorème des valeurs intermédiaires
- Une fonction continue sur un intervalle qui prend deux valeurs m et n, prend également toutes les valeurs intermédiaires.
- Théorème de la bijection
- Une fonction continue et strictement monotone sur un intervalle constitue une bijection entre cet intervalle et son image. Toute valeur de l’intervalle admet une solution unique.
Fonctions composés
- Propriétés des fonctions composées
- Si f croissante et g croissante alors croissante.
- Si f décroissante et g décroissante alors croissante.
- Si f croissante et g décroissante alors décroissante.
- Si g croissante et f décroissante alors décroissante.
Dérivées et primitives
- Dérivée
- D’un point de vue géométrique, c’est le coefficient directeur (pente) de la tangente d’une courbe en un point.
- Primitive
- Anti-dérivée, Fonction F définie sur I telle que :
Lettres et symboles
Ensembles de définition
| Lettre | Ensemble | Quelques valeurs |
|---|---|---|
| Entier naturels | 0, 8, 16, 103 | |
| Entiers relatifs | -23, 0, 14, 28 | |
| Rationnels (fractions de nombres entiers) | 1, 5/4, -214/34 | |
| Réels | -1.2114, 23, 3656.24 | |
| Corps des nombre complexes | -6.6, 21, 3i, 4i+6.7 |
Lettres grecs
| Lettre grec | Nom |
|---|---|
| Alpha | |
| Beta | |
| Gamma | |
| (maj. ) | Delta |
| Epsilon | |
| Theta | |
| Lambda | |
| Mu | |
| Pi | |
| Rho | |
| (maj. ) | Sigma |
| Tau | |
| Phi | |
| (maj. ) | Omega |
Utilisations usuelles des symboles
| Symbole | Utilisation usuelle |
|---|---|
| Solutions réelles sur un intervalle donné | |
| Discriminant d’un polynôme | |
| ~3.14, utilisé en trigonométrie | |
| variable | |
| Angle sur le cercle trigonométrique | |
| A, B, C, D | Point géométriques |
| A’, B’, C’, D’ | Images/Transformés de points |
| I, J | Milieux de segment |
| M, N | Points aléatoires en géométrie |
| P, Q | Matrices |
| f,g,h | Fonctions |
| f’,g’,h’ | Fonctions dérivées |
| F,G,H | Fonctions primitives |
| i | Unité imaginaire |
| k | Constante réel ou entier relatif |
| n | Entier naturel |
| x | Abscisse, variable |
| y | Ordonné, solution de fonction affine |
| z | Nombre complexe, coordonnée dans l’espace |


